Sustainability in rangeland systems: Introduction of fuzzy multi objective decision making
Hossein Azadi1 * , Jan Van Den Berg2 , Peter Ho1 and Gholamhossein Hosseininia3
1
Centre for Development Studies,
Faculty of Spatial Sciences,
University of Groningen,
The Netherlands
2
Faculty of Technology,
Policy, and Management, Section of ICT,
Delft University of Technology,
The Netherlands
3
Deputy of Research,
Education and Extension,
Ministry of Cooperative,
Tehran,
Iran
DOI: http://dx.doi.org/10.12944/CWE.4.1.04
It is widely recognized that approaching sustainability in rangeland management needs to take many criteria into consideration which unavoidably calls for the application of multi-criteria decision making approach. Bearing conflicting objectives in mind, which are mainly conservation and utilization, we have introduced fuzzy multi-objectives decision making as a suitable approach when sustainability in rangeland management is a goal. While some extensions of the approach are discussed, interactive fuzzy multi objective linear programming, and a framework including three stages are presented to make it more applicable. The proposed approach in this paper comprises three important advantages for decision makers to apply: first, it is a useful tool to involve trade-offs analysis between the conflicting objectives; second, it challenges to uncertainty of any decision in sustainable rangeland management; and third, it considers existing alternatives under given constraints by developing new alternatives for all possible situations.
Copy the following to cite this article:
Azadi H, Berg J.V.D, Ho P, Hosseininia G. Sustainability in rangeland systems: Introduction of fuzzy multi objective decision making. Curr World Environ 2009;4(1):19-32 DOI:http://dx.doi.org/10.12944/CWE.4.1.04
Copy the following to cite this URL:
Azadi H, Berg J.V.D, Ho P, Hosseininia G. Sustainability in rangeland systems: Introduction of fuzzy multi objective decision making. Curr World Environ 2009;4(1):19-32. Available from: http://www.cwejournal.org/?p=881
Download article (pdf)
Citation Manager
Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 2009-04-06 |
|---|---|
| Accepted: | 2009-05-04 |
Introduction
Land degradation and overgrazing are nowadays two main fundamental threats in rangeland systems (Box 2002; Buss and Nuppenau 2002; Howery et al., 2000; Miller 2005; Walker and Hodgkinson 2000). Consequently, their current capability to produce edible forage for livestock is less than their potential1 (Azadi 2005; Umrani 1998). Globally, rangelands are at risk from numerous pressures (Mitchell et al., 1999) mainly arising from inappropriate rangeland management systems. The science of rangeland management should develop in order to be able to guarantee a sustainable future. In this regard, achieving equilibrium2 in rangeland systems is the most important challenge in sustainable rangeland management (SRM) (Azadi 2005; Walker 1995).
When a rangeland is overgrazed, the rationale and common approaches to SRM are increasingly criticized and equilibrium in rangeland systems gets disputed (Walker 1995). Achieving equilibrium could yet be possible once its concept and terminology are well-understood. The understanding of the complex notion of equilibrium in SRM has already been place of many debates (Box 1995; 2002; Buss and Nuppenau 2002; Deadman 1999; Roe 1997; Walker and Hodgkinson 2000) which embraces several other concepts related to timely management decision (Redfearn and Bidwell 2004). If carrying capacity,1 for instance, is not close to the proper level related to equilibrium rate, regardless of employed grazing systems, objectives of equilibrium in a rangeland system will not be met (Roe 1997).
The recent literatures on SRM call in question for any specific measures of equilibrium, whether the range is stocked or unstocked, managed or mis-managed (Box 2002; Redfearn and Bidwell 2004). The equilibrium of a given area can then be varied according to “management decisions” (Kenny 2004) which would (in)directly deal with several criteria i.e., techno, eco, socio, and economic. As a result, equilibrium in a rangeland system is basically a Multi Objective Decision Making (MODM) where the two main objectives are maximizing rangelands ‘conservation’ on the one hand, and their ‘utilization’, on the other. MODM is especially recognized when resources attribution is a goal (Lu et al., 2007). Optimizing the decisions on rangeland resources will hence be the cause of equilibrium-disequilibrium and therefore, direct decision makers –mainly policy makers and pastoralists- to SRM in a long-run action.
While MODM could be appreciated as a useful technique to involve trade-offs analysis between conflicting objectives (Hwang and Yoon 1981; Malczewski 2001) as here, conservation and utilization, one may point to the uncertainty of any decision-making situation which is inevitable at all levels of human interaction with the environment. In the broad area of applied sciences and, particularly in rangeland systems, many processes are never clear-cut (Azadi 2003). Indeed, in environmental systems, a practitioner or researcher has to cope with many forms of uncertainty, including subjective estimation and perception (Azadi et al., 2005; Clark and Gelfand 2006), the complexity of modeling (Wainwright and Mulligan 2004), interaction of subsystems (Deaton and Winebrake 2000), lack of precise values (Silvert 1997; 2000), missed data and limited information (Srebotnjak 2007), processing data deficiencies (Lawrence 2003), or ambiguities in natural language.
Likewise, in rangeland management, this uncertainty is enhanced by the fact that many policy-makers often judge based on their personal experience and background (Azadi et al., 2007). As several types of uncertainty including, imprecision and ambiguity are inherently present in natural systems, traditional system methodologies like probability theory and statistics cannot adequately model many of these systems (Checkland 1990) often artificially imposed precision or theoretical assumptions only result in increasing the complexity of the model (Wang et al., 1998).
As Lai and Hwang (1995) previously discussed, fuzzy multi objective models can help decision-makers by considering existing alternatives under given constraints, and by developing new alternatives for all possible situations. They believe that the effectiveness of a decision makers’ performance in a decision process can be improved as a result of the high quality of analytic fuzzy numbers. Here, in the complex context of SRM, decisions should be made based on imprecise information (Batabyal and Godfrey 2002; Umrani 1998). Since a decision in the area of SRM is usually vague, it can be best modeled based on fuzzy set theory (Petrovic-Lazarevic and Abraham 2003). This paper aims to introduce an extended version of Fuzzy MODM to approach sustainability in rangeland management.
Origin and Backgrounds
Rangeland management concerns an interdisciplinary approach (Aenis and Nagel 2000; Azadi et al., 2003). Determination of optimum land use to approach sustainability involves analysis of data from both hard sciences1 (e.g. soil science) to soft sciences2 (e.g. social science) and earlier asked for creating inter-disciplinary (Shaner et al., 1982) while recently calls for trans-disciplinary approaches (Chartrand 2006). All these paradigmatic changes (Kuhn 1962) have been adopted by separate schools (Sands 1986) who often claim to use inimitable methodology (if don’t sharply declare unique epistemology and especially, ontology)3 which takes various criteria into their analyses. All the criteria are however, not equally important; every criterion can therefore be contributing towards SRM at a different degree (Azadi et al., 2005). In addition, SRM involves major decisions at various levels, most importantly determining stocking rate4, vegetation density, topography, estimating right rate of stocking for each class of pasture, agreement between (either homogenous or heterogeneous) experts (Azadi et al., 2007). The present popular methods in assessing SRM commonly include techno-socio-economic criteria (both qualitative and quantitative). Those (Azadi et al., 2003; Azadi 2005; Box 2002; Buss and Nuppenau 2002; Howery et al., 2000; Miller 2005; Walker and Hodgkinson 2000) who tried to include all the three major dimensions of SRM, have neglected to include ranking and ratings, weighted summation, requirement matching etc in their estimations. Here the weights are arbitrarily chosen, and are aggregated using simple Boolean overlay methods. Although these methods are simple and straightforward, they suffer from solid mathematical foundations. Furthermore, the multi-criteria SRM was previously assessed spatial homogeneity over the area under study (e.g. Box 1995; 2002; Buss and Nuppenau 2002; Deadman 1999; Hiernaux 1996; Hodgkinson 1996; Howery et al., 2000; Kopp 2004; Walker and Hodgkinson 2000). This is often unrealistic if the study of land suitability in general, or SRM in particular, are the goals. In complex systems, as Malczewski (1999) discussed, the decisions should be made using criteria which vary across in space. To deal with the spatial decision making in this context, MCE1 and GIS2 can also be integrated (Jankowski 1995). Broadly used MCE methods in the (range)land sustainability analysis are ranking and rating. The techniques however, suffer from a strong theoretical foundation for determining the weights as they assign the weights rather arbitrarily. More specifically, they pass over any comparison among the criteria and indicators. Likewise, the outcomes of such analyses are aggregated using (simple) Boolean superimpose or weighted aggregation (Cornelissen 2001) which ends up in strict (black and white) decisions.
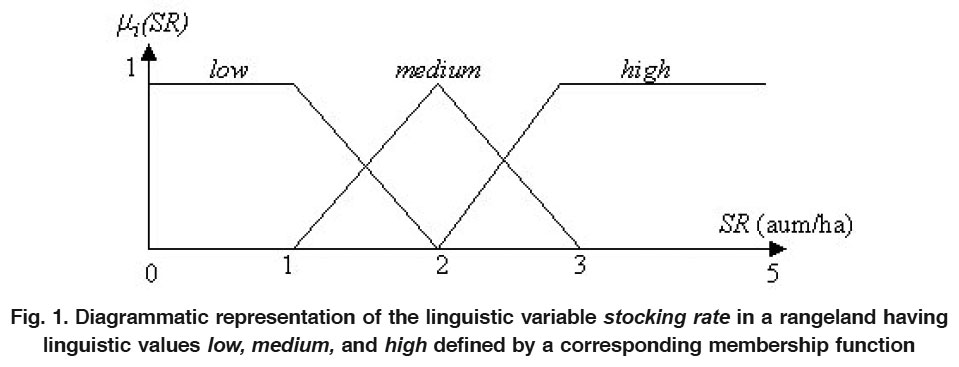 |
Figure 1. Diagrammatic representation of the linguistic variable stocking rate in a rangeland having linguistic values low, medium, and high defined by a corresponding membership function Click here to view figure |
In so doing, the ranking and rating techniques are criticized as not properly reflecting the decision maker’s views nor having enough rational support behind the approach (Stuth and Lyons 1993). According to ‘Principle of Incompatibility’, “as the complexity of a system increases, human ability to make precious and relevant (meaningful) statements about its behavior diminishes until a threshold is reached beyond which the precision and the relevance become mutually exclusive characteristics” (Zadeh 1973: 29). It is therefore, that fuzzy statements are the excellent bearers of meaning and relevance. Zadeh used this principle for extending the applicability of his fuzzy sets theory and fuzzy logic to the analysis of complex systems. It is now realized that complex real-world problems require intelligent systems that combine knowledge, techniques, and methodologies from various sources. These intelligent systems are supposed to do better in changing environments, and to explain how they make decisions or take actions (Jang et al., 1997). Ecological studies are known to be complex in nature (Silvert 1997) and therefore fuzzy logic seems to be an appropriate technique to solve the dichotomy that is inherent in sustainability of natural resources (Andriantiatsaholiniaina 2001; Cornelissen et al., 2001; Dunn et al., 1995; Marks et al., 1995) including rangeland management (Azadi 2003; 2005; Azadi et al., 2005; Azadi et al., 2007)
Foundations of Fuzzy Logic
Some basic foundations of fuzzy logic is discussed in our previous works (Azadi et al., 2005; Azadi et al., 2007). Here, we review the minimal information needed to end-up with the extension of Fuzzy MODM.
Crisp Models
In quantitative sciences where mathematical models are used for analyzing real-world phenomena, (stochastic) variables are introduced having a ‘well-defined’ meaning. During their scientific work, the corresponding scientists apply mathematical tools from calculus, from the theory of differential equations, from discrete mathematics, from (vector) algebra, from numerical methods, from (complex) function theory, and more (van den Berg 2004). The resulting models offer an ‘idealized’ world, an ‘objective and structured reality’ with, hopefully, rather general validity. Uncertainty is usually described in probabilistic and statistical terms like probabilities on crisp events (i.e. events that do occur or do not occur at all), expected values, statistical tests (that are either rejected or not rejected), interval estimations, et cetera (Zimmermann 1996). Propositions within these approaches are usually supposed to be either true or false (and sometimes unknown). In line with this way of working as applied in physics, chemistry, econometrics, and other ‘hard sciences’, the first knowledge-based systems developed in the community of Artificial Intelligence were founded on the ‘physical symbol system hypothesis’ expressing that symbols (and only symbols) can represent states of the world and statements about the world. Again, the only ‘epistemological commitments’ allowed for these statements are either true, false or unknown. The physical symbol system hypothesis has still to be proven (van den Berg 2004).
 |
Figure 2: Building blocks of a Fuzzy Inference System (FIS) Click here to view figure |
Boolean vs. Fuzzy
Three hundred years B.C., the Greek philosopher, Aristotle came up with binary logic (0,1), which is now the principle foundation of Mathematics. It came down to one law: A or not A, either this or not this. For example, a typical rose is either red or not red. It cannot be red and not red. Every statement or sentence is true or false or has the truth-value 1 or 0. This is Aristotle’s law of bivalence and was philosophically correct for over two thousand years (Kosko 1993).
Two centuries before Aristotle, Buddha, had the belief which contradicted the black-and-white world of worlds, which went beyond the bivalent cocoon and see the world as it is, filled with contradictions, with things and not things. He stated that a rose, could be to a certain degree completely red, but at the same time could also be at a certain degree not red. Meaning that it can be red and not red at the same time. Conventional (Boolean) logic states that a glass can be full or not full of water. However, suppose one were to fill the glass only halfway. Then the glass can be half-full and half-not-full. Clearly, this disproves Aristotle’s law of bivalence. This concept of certain degree or multivalence is the fundamental concept, which propelled Zadeh at the University of California in 1965 to introduce fuzzy logic. The essential characteristics of fuzzy logic founded by him are as follows (Abdul Aziz 1996):
- In fuzzy logic, exact reasoning is viewed as a limiting case of approximate reasoning,
- In fuzzy logic everything is a matter of degree,
- Any logical system can be fuzzified,
- In fuzzy logic, knowledge is interpreted as a collection of elastic or, equivalently, fuzzy constraint on a collection of variables, and
- Inference is viewed as a process of propagation of elastic constraints.
The third statement hence, defines Boolean logic as a subset of Fuzzy logic.
Towards Soft Computing
It is clear from history that the hard sciences have been and still are quite successful in many areas. Based on this success, they have obtained a strong and predominant position and many scientists working in this field seem to believe that their approach of crisp, two-valued logical, precise mathematical modeling where uncertainty is modeled within a probabilistic, statistical framework, is the one and only true, applicable approach (van den Berg 2004).
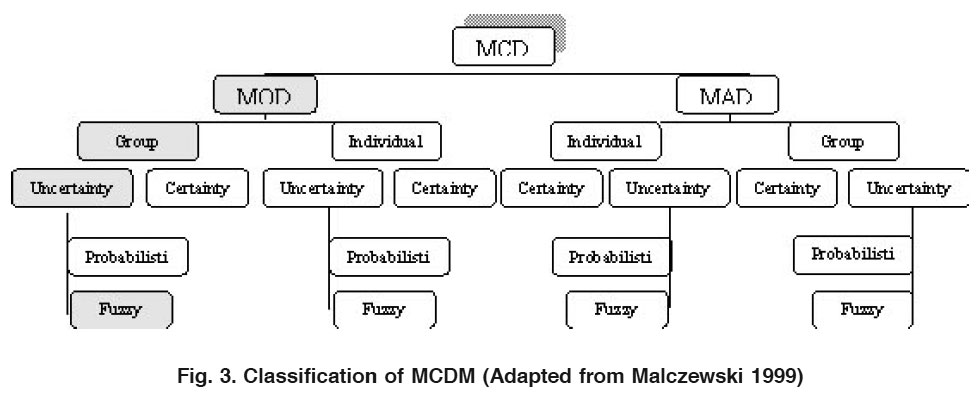 |
Figure 3. Classification of MCDM (Adapted from Malczewski 1999) Click here to view figure |
For several reasons, however, like ‘irrelevance’ and ‘complexity’, one may doubt whether hard computing is always the right tool. Considering ‘Principle of Incompatibility’, we try to answer the following series of questions related to problems with increasing complexity. They may convince you of the validity of Zadeh’s principle: (1) How sustainable is a rangeland? (2) Which measures are important in SRM? (3) How much is the stocking rate of a sustainable rangeland? (4) How much is its vegetation density? (5) How much annual rainfall is needed in a sustainable rangeland? (6) How many pastoralists’ families can live in the world of Artificial Intelligence, similar lessons have been learned. While, implementing systems based on ideas like the above-mentioned physical symbol hypothesis, problems arose related to the modeling of the likeliness of a certain conclusion and to the lack of robustness and flexibility. Apparently, the tools as made available by the hard sciences also have their limitations when trying to apply ‘intelligent techniques’. In several cases, it has been shown that alternative approaches with fuzzy or other ‘vague’ ingredients work better. Successful fuzzy modeling projects exist since 1975 on topics like automatic control, printed character recognition, target selection for marketing purposes, financial modeling, SD, and more (van den Berg 2004).
Linguistic Variables
Fuzzy logic enables the modeling of expert knowledge. The key notion to do so is that of a linguistic variable (instead of a quantitative variable) which takes linguistic values (instead of numerical ones). For example, if stocking rate (SR) in a rangeland is interpreted as linguistic variable, then its linguistic values could be one from the so-called term-set T(SR) = {low, medium, high} where each term in T(SR) is characterized by a fuzzy set in the universe of discourse, here, e.g., U = [0, 5]. We might interpret low as a “stocking rate of less than approximately 1.5 aum/ha”, medium as a “stocking rate close to 2 aum/ha”, and high as a “stocking rate of roughly more than 2.5 aum/ha” where the class boundaries are fuzzy. These linguistic values are characterized by fuzzy sets whose membership functions are shown in Fig. 1.
Knowledge Representation by Fuzzy IF-Then Rules
Fuzzy logic is a scientific tool that permits simulation of the dynamics of a system without a detailed mathematical description. In an expert-driven approach, knowledge is represented by fuzzy IF-THEN linguistic rules having the general form
If x1 is A1 AND x2 is A2 AND xm is Am THEN y is B,
where x1, … , xm are linguistic input variables with linguistic values A1, … , Am respectively and where y is the linguistic output variable with linguistic value B.
To illuminate we consider animal unit and vegetation density as the principal factors for having equilibrium. Then the relevant fuzzy rules could be:
- If amount of animal unit is low and vegetation density is poor Then equilibrium is medium.
- If amount of animal unit is medium and vegetation density is poor Then equilibrium is weak.
- If amount of animal unit is high and vegetation density is poor Then equilibrium is very weak.
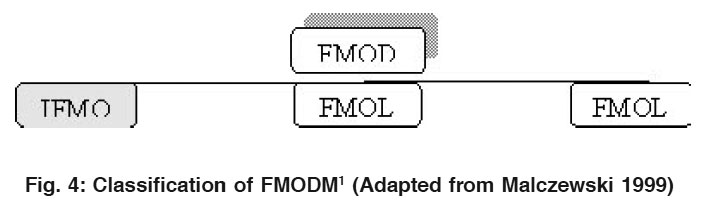 |
Figure 4: Classification of FMODM1 (Adapted from Malczewski 1999) Click here to view figure |
Architecture of Fuzzy Systems
Fuzzy Inference Systems or, shortly, Fuzzy Systems (FSs) usually implement a crisp input-output (IO) mapping consisting of basically four units, namely
- A Fuzzifier transforming crisp inputs into the fuzzy domain,
- A Rule Base of fuzzy IF-THEN rules,
- An Inference Engine implementing fuzzy reasoning by combining the fuzzified input with the rules of the Rule Base,
- A Defuzzifier transforming the fuzzy output of the Inference Engine to a crisp value (Fig. 2).
In some practical systems, the Fuzzifier or the Defuzzifier may be absent namely in cases where fuzzy input data are available or the fuzzy system output can be interpreted directly in linguistic terms. Corresponding “approximate reasoning techniques” are available (see, e.g. Jang et al., 1997).
Fuzzy Reasoning
Probably, the hardest part to understand is the precise way fuzzy reasoning can be implemented. An extensive discussion of this topic is outside the scope of this dissertation so we limit ourselves here to present just the basic idea. Classical logic is our starting point using the classical reasoning pattern ‘modus ponens’:
Given fact “x is A” and rule “IF x is A, THEN y is B”, we conclude “y is B”.
“Applying fuzzy reasoning, classical modus ponens can be generalized to an ‘approximate reasoning’ scheme of type.”
Given fact “x is A’ “ and rule “IF x is A, THEN y is B”, we conclude that “y is B’ “.
Here, the assumption made is that the closer A’ to A, the closer will B’ be to B. It turns out that especial combinations of operations on fuzzy sets like ‘max-min’ and ‘max-product’ composition can fulfill this requirement. The complete fuzzy reasoning in a FS can be set up as follows:
- The fuzzification module calculates the so-called ‘firing rate’ (or degree of fulfillment) of each rule by taking into account the similarity between the actual input A’ defined by membership function mA’(x) (and in case of a crisp input xp defined by the value mA(xp) and the input A of each rule defined by membership function mA(x).
- Using the firing-rates calculated, the inference engine determines the fuzzy output B’ for each rule, defined by membership function mB’(y).
- The inference engine combines all fuzzy outputs B’ into one overall fuzzy output defined by membership function m(y).
- The defuzzification module calculates the crisp output yp using a defuzzification operation like ‘centroïd of gravity (area)’.
For a treatment in depth on FSs, its construction and corresponding reasoning schemes (including the most popular systems like Mamdani (Mamdani and Gaines 1981) and Tagaki-Sugeno Fuzzy Models (Tagaki and Sugeno 1985), we refer to the above-mentioned textbooks.
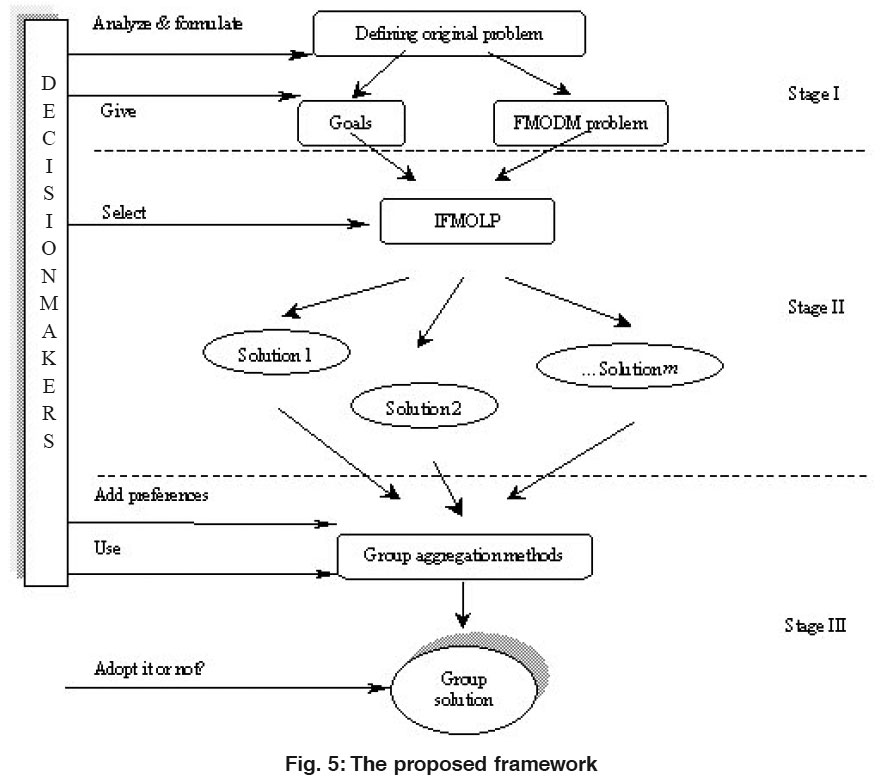 |
Figure 5: The proposed framework Click here to view figure |
Foundations of Multi Criteria Decision Making
Multi Criteria Decision Making (MCDM) is a well-known branch of decision making (Malczewski 1999). The range of the MCDM approaches are previously from simple technical application problems to currently more complicated eco-socio-economic problems (Lu et al., 2007). It is a branch of a general class of operations research models which deal with decision problems under the presence of a number of decision criteria (Petrovic-Lazarevic and Abraham 2003). Decision making is a set of systematic procedures for analyzing complex decision problems. These procedures include dividing the decision problems into smaller and more understandable parts; analyzing each part; and integrating the parts in a logical manner to produce a meaningful solution (Grünig, and Kühn 2005). The process of MCDM is always confused by decision makers, because there is always a trade-off between all criteria. MCDM system can usually help decision makers quantify and evaluate each criterion and rank all alternatives. In general, MCDM approches involve six components (Keeney and Raiffa 1976; Pitz and McKillip 1984):
- A goal or a set of goals the decision maker wants to achieve (e.g. in SRM. how to approach equilibrium holding utilization and conservation),
- The decision maker or a group of decision makers involved in the decision making process with their preferences with respect to the proposed criteria (e.g. in SRM, homogenous and heterogeneous experts/ decision makers having different beliefs how to approach SRM),The set of decision alternatives (e.g. in SRM, in/decreasing carrying capacity1),The set of uncontrollable (independent) variables or states of nature (e.g. in SRM facing drought),
- A set of proposed criteria (e.g. in SRM, different techno-socio-economic criteria),
- The set of outcomes or consequences associated with each alternative attribute pair (e.g. in SRM, rangeland degradation/revival).
MODM and MADM
Two basic approaches to MCDM problems can be distinguished: Multiple Attribute Decision Making (MADM) and Multiple Objective Decision Making (MODM) (Climaco 1997; Pohekar and Ramachandran 2004).The distinction between MADM and MODM is related to the evaluation criteria which are the standards of judgments (or rules) on which the alternatives are ranked according to their desirability (Lu et al., 2007). The key feature of the MCDM framework, whether under MODM or MADM, is that tradeoffs among the various objectives are explicitly analyzed (Hwang and Yoon 1981).
MADM problems require that choices are being made among alternatives described by their attributes. It is therefore, a useful technique to choose the best among different alternatives. The set of attributes is given explicitly and multi-attribute problems have a finite set of feasible alternatives (Table 1). Here in SRM, MADM can be usable when (e.g.) pastoralists would like to know the best specie(s) of livestock who can survive in an optional pasture.
Unlike MADM, MODM problems explicitly deal with the relationship of attributes of alternatives to higher level objectives. MODM involves designing the alternatives and searching for the best decisions among an infinite or very large set of feasible alternatives. Each alternative is defined implicitly in terms of the decision variables and evaluated by means of objective functions (Malczewski 1997) which can here be considered as (e.g.) utilization and conservation functions.
 |
Table 1: Comparison of MODM and MADM Approaches (Adapted from: Hwang and Yoon 1981; Starr and Zeleny 1977) Click here to view table |
The main difference between MODM and MADM models can yet be explained by the MODM’s focus on decision problems with ‘continuous’ decision space while MADM’s focus is with problems of ‘discrete’ nature (considering stocking rate as the most effective determinant of carrying capacity in SRM, we are faced continuous decision space). Furthermore, MODM models generally deal with resources attribution (e.g. natural resource management including rangelands), whereas MADM models often deals with evaluating several predefined choices and coming up with the best at last (Lu et al., 2007).
There are several methods in each of the two categories. Priority based, outranking, distance based and mixed methods which are all applied to various problems. Each method has its own characteristics and the can be classified as deterministic, stochastic and fuzzy (Pohekar and Ramachandran 2004). There may also be combinations of the above methods. Depending upon the number of decision makers, the methods can be classified as single or group decision making methods. Decision making under uncertainty and decision support systems are also prominent decision making techniques (Gal and Hanne 1999). MCDM techniques can be used to identify a single most preferred option (e.g. conservation in SRM), to rank options (e.g. first conservation, and then utilization in SRM), to list a limited number of options for subsequent detailed evaluation (e.g. different climax or species of livestock in SRM), or to distinguish acceptable from unacceptable possibilities (e.g. zero grazing, grazing, overgrazing in SRM). There are many MCDM approaches which differ in how they combine and utilize the data. MCDM approaches can be classified on the basis of the major components of multi criteria decision making. Malczewski (1999) made three following layered classificationsas sketched on Fig. 3:
- MODM versus MADM
- individual versus group decision maker problems, anddecisions under certainty versus decisions under uncertainty,1 this ‘uncertain’ context can more comprehensively understood. Finally, the ‘fuzzy’ nature of different SRM criteria directs us to follow the grey area of Fig. 3 when approaching equilibrium is the goal.
As discussed in the previous sections, equilibrium in rangeland system can better be approached using ‘MODM’. Calling heterogeneous ‘group’ of experts (Azadi et al., 2007) in the framework of stakeholder approach
Extension of Fuzzy MODM Models
Most MODM problems can be formulated by multi objective linear programming (MOLP) models. Refereeing to the imprecision and insufficient inherent in human judgments (Silvert 1997; 2000), uncertainties may be affected and incorporated in the parameters of an multi-objective linear programming model, which is called a Fuzzy MOLP (FMOLP) model. Uncertainties are also involved in the goals of decision makers for their multiple objectives, called fuzzy multi-objective linear goal programming (FMOLGP). According to Lu et al., (2007), the FMODM models extend MODM decision functions from crisp to imprecise scope. In this regard, they discuss about two essential issues as follows:
- In the proposed FMOLP model, fuzzy parameters may appear in both objective functions and constraints. If only objective functions or only constraints include fuzzy parameters, the model would still be applicable to deal with non-fuzzy parameters, as a real number is as a special case of a fuzzy number. Similarly, in the proposed FMOLGP, a goal with a real number is also as a special case of a fuzzy goal.
- Both FMOLP and FMOLGP models, allow decision makers to use any form of membership functions for describing fuzzy parameters in objective functions and constraints, and fuzzy goals.
Methods
As already described, FMOLP is the most popular form of FMODM models. To drive an optimal solution for an FMOLP problem, as Lu et al., (2007) described, three FMLOP methods can commonly be used, as follows (Fig. 4):
- FMOLP, a non-interactive method, which can directly generate an optimal solution,1
- FMOLGP, which integrates fuzzy sets with goal programming to extend multi-objective decision analysis, and
- Interactive FMOLP (IFMOLP) method, which has both interactive and goal features (as projected for this proposal).1 for the FMODM problem. And the third one is about the different processes of solving the FMODM problem.
There are three issues involved in the development of an FMODM method (see Lu et al., 2007; p. 123-125). The first issue is about how to express fuzzy parameters of objective functions and constraints and fuzzy goals by membership functions. The second one is about the presentation of form of Pareto optimal solution1 for the FMODM problem. And the third one is about the different processes of solving the FMODM problem.
For the first issue, as shown by Azadi et al., 2007 in a field study, fuzzy values of parameters are often generated by some (homo/ heterogeneous) experts and therefore have different figures of data distributions. Some of them may be suitable to be described in a triangular form of membership functions, and some may be more suitable to be expressed in other forms such as a trapezoidal one.
The second issue involves the expression of a solution and corresponded objective values for the FMODM problem. If an FMDOM method is to provide us with useful assistance, its output, an optimal solution with optimal objective values, must be of sufficient quality and in a suitable form for the decision we are concerned to make (e.g. tuning Stocking Rate to optimize carrying capacity in SRM). The third issue is about the process of finding an optimal solution (here in SRM, optimal solution should include some degrees of both utilization and conservation). This issue involves understanding the preferences of some decision makers involved the solution process of an MODM problem. It has been found that there are obvious different priorities for decision makers for the process of finding an optimal solution (Azadi et al., 2007) for an FMODM problem. Some decision makers expect to have a method that can fast generate an optimal solution for a given FMODM problem without any extra data providing from them. While others have goals for their decision objectives in their FMODM problem and therefore, prefer a method that can find an optimal solution, which can maximize to meet these goals (e.g. in SRM, maximizing both utilization and conservation). Finally, with the support of software, some decision makers desire to have a chance to explore more alternative solutions in an interactive fashion with the aim of meeting the goals by finding a satisfying solution. They may then desire to be allowed to continuing revise their goals or change the weights of objective functions, so that to get new optimal solutions.
Proposed Framework
It’s been expected that the proposed framework effectively integrates a series of techniques and concepts to help decision makers to obtain a comprehensive and more ‘sustainable’ results in the field. The framework entails three stages as shown in Fig. 5:
Stage I
In Stage I, a decision group of SRM is set up and an FMODM problem including its variables, objectives, and constraints are determined. Each expert can define his/her expectations or weights to the predefined objectives of SRM, which are used to generate individual solutions to the FMODM problem.
Stage II
The expert, in Stage II, obtains an optimal solution by using a suitable FMODM method (i.e. here IFMOLP) under their goals and preferences among several methods that are available. They then state their solutions and aspiration levels for each objective – i.e., conservation and utilization- into the group.
Stage III
Finally, in Stage III, these individual solutions are as alternatives to form group’s solution for the problem. The decision group members exchange their ideas, express their preferences and judgments on the alternatives, and identify desirable solutions. Each expert is given a weight, if it needs, and a utility group aggregation method is then used to determine the ‘best’ alternative, a compromise solution in general, to the FMODM problem through aggregation of individual solutions and their weights (to generate the group solution, each expert’s individual solution may be given an equal or non-equal priority).
Conclusion
The proposed approach in this paper comprises three important advantages for decision makers to apply: first, it is a useful tool to involve trade-offs analysis between conflicting objectives including conservation and utilization; second, it challenges to uncertainty of any decision in SRM; and third, it considers existing alternatives under given constraints by developing new alternatives for all possible situations. The approach, therefore, has the potential to become a practical tool to policy-makers and scientists. At last, it is important to note that we are aware that the proposed framework is built theoretically and should be considered as the first step. It has to be strongly validated in the field, as a several case studies in which we have a plan to apply for one. However, the existing flexibility in the second stage of the framework is one of its advantages in which provides a new useful tool for decision makers to adjust their decisions based upon other possible solution(s).
References
- Abdul Aziz S., You fuzzyin’ with me? Available on: http://www.doc.ic.ac.uk/~nd/surprise_96/ journal/vol1/sbaa/article1.html (1996).
- Aenis T and Nagel UJ., Participatory management of large interdisciplinary research teams - First experiences from a rural research and development project in Germany. Available on: http://www.zalf.de/ home _ zalf/sites/grano/publikation/ aenisnagel2000.pdf (2000)
- Andriantiatsaholiniaina LA., Sustainability Assessment Using Fuzzy Logic. Ph.D. Dissertation. Chania: Department of Production Engineering and Management, Technical University of Crete, Greece (2001).
- Azadi H., Explaining Equilibrium between Livestock and Rangeland Using Fuzzy Logic. PhD dissertation. Shiraz: Shiraz University (2005).
- Azadi H, Shahvali M and Faghih N., Using fuzzy logic in solving conflict between sustainability and pasture. The Proceedings of the 4th Seminar on Fuzzy Sets and its Applications, 1-15. May 28-29, 2003, University of Mazandaran, Babolsar, Iran (2003).
- Azadi H, Shahvali M and van den Berg J., Sustainable rangeland management: A new paradigm for rangelands extensionists. International Journal of Extension Systems (2005) 22: 27-38.
- Azadi H, Shahvali M, van den Berg J and Faghih N., Sustainable rangeland management using a multi-fuzzy model: How to deal with heterogeneous experts’ knowledge. Journal of Environmental Management (2007)83: 236-249.
- Batabyal AA and Godfrey EB., Rangeland management under uncertainty: A conceptual approach. Journal of Range Management (2002) 55: 12-5.
- Box TW., Private Property Rights and Sustainable Rangeland Use. University of California: Center for Forestry, UC Berkeley (1995).
- Box TW., Future deserts and sustainable communities. Available on: http://www.rala.is/ rade/ralareport/Box.pdf (2002).
- Buss HJ and Nuppenau EA., More sustainable range use in semi-arid eco-systems through adapted management: A case study on Namibian farms based on bio-economic models. Contributed Paper and Poster, Deutscher Tropentag 2002, Witzenhausen, 9. bis 11. October (2002).
- Chartrand HH., Ideological Evolution. The Competitiveness of Nations in a Global Knowledge-Based Economy. An Individual Interdisciplinary Studies PhD Dissertation. Canada: University of Saskatchewan (2006).
- Checkland PB., The Origins and Nature of Hard Systems Thinking. England: The Open University Press (1980).
- Checkland PB., Soft Systems Methodology in Action. New York: John Wiley & Sons Ltd (1990).
- Clark JS and Gelfand AE., A future for models and data in environmental science. TRENDS in Ecology and Evolution (2006) 21: 375-380.
- Climaco J., Multicriteria Analysis. New York: Springer (1997).
- Cornelissen AMG, van den Berg J, Koops WJ, Grossman M and Udo HMJ., Assessment of the contribution of sustainability indicators to sustainable development: A novel approach using fuzzy set theory. Agriculture, Ecosystems and Environment (2001) 86: 173-185.
- Deadman PJ., Modeling individual behavior and group performance in an intelligent agent based simulation of the tragedy of the commons. Journal of Environmental Management (1999) 56: 159-172.
- Deaton ML and Winebrake JJ., Dynamic Modeling of Environmental Systems. New York: Springer (2000).
- Dunn EG, Keller JM, Marks LA, Ikerd JE, Fader PD and Godsey LD., Extending the application of fuzzy sets to the problem of agricultural sustainability. IEEE Proceedings of ISUMA-NAFIPS ’95, Missouri-Columbia, USA (1995).
- FAO., A framework for land evaluation. FAO Soils bulletin 32. Available on: http://www.fao.org/docrep/X5310E/x5310e00.htm#Contents (1976).
- Friedman MT and Mason DS., A stakeholder approach to understanding economic development decision making: public subsidies for professional sport facilities. Economic Development Quarterly (2004) 18: 236-254.
- Gal T, Hanne T., Multi criteria decision making: Advances in MCDM models, algorithms, theory, and applications. New York: Kluwer Academic Publishers (1999).
- Glossary of Terms Used in Range Management., Range sites of Florida. Glossary of terms used in range management. Available on: http:// wfrec.ifas.ufl.edu/range/rangelands/glossary.htm (2002).
- Grünig R and Kühn R., Overview of Decision-Making Procedure. Successful Decision-making. A Systematic Approach to Complex Problems. New York: Springer (2005).
- Heron J and Reason P., A participatory inquiry paradigm. Qualitative Inquiry (1997) 3: 274-294.
- Hiernaux P., The Crisis of Sahelian Pastoralism: Ecological or Economic? ODI Pastoral Development Network Paper 39a. 20p. London: Overseas Development Institute (1996).
- Hodgkinson KC., A model for perennial grass mortality under grazing. In: N.E. West (Ed.), Rangelands in a Sustainable Biosphere. Proceedings Vth International Rangeland Congress, Denver: Society for Range Management (1996) 1: 240-241.
- Howery LD, Sprinkle JE, and Bowns JE., A Summary of Livestock Grazing Systems Used on Rangelands in the Western United States and Canada. Cooperative Extension, College of Agriculture & Life Sciences, The University of Arizona (2000).
- Hwang CL and Yoon K., Lecture Notes in Economics and Mathematical Systems: Multiple Attribute Decision-Making. New York, Springer (1981).
- Jang JSR, Sun CT and Mizutani E., Neuro-Fuzzy and Soft Computing, A Computational Approach to Learning and Machine Intelligence. Prentice Hall (1997).
- Jankowski P., Integrating geographical information systems and multiple criteria decision making methods. International Journal of geographic Information System (1995) 3: 251-273.
- Keeney RL and Raiffa H., Decisions with Multiple Objectives: Preferences and Value Tradeoffs. New York: John Wiley & Sons (1976).
- Kenny G., Report to the productivity commission. Cost and stocking rate data for the Murweh Shire. Available on: http:// www.pc.gov.au/inquiry/nativevegetation/ consultancy/murweh1/murweh1.pdf (2004).
- Kopp J., Stocking Rates and AUM-Frequently Asked Questions. Alberta government. Department of Agriculture, Food and Rural Development (2004).
- Kosko B., Fuzzy Thinking. New York: Hyperion (1993).
- Kuhn T., The Structure of Scientific Revolutions. Chicago: University of Chicago Press (1962).
- Lai YJ and Hwang CL., Fuzzy Multi Objective Decision Making: Methods and Applications. Berlin: Spinger -Verlag (1995).
- Lawrence DP., Environmental Impact Assessment: Practical Solutions to Recurrent Problems. New York: John Wiley & Sons, Inc (2003).
- Lu J, Zhang G, Ruan D and Wu F., Multi-objective Group Decision Making. Methods, Software, and Applications with Fuzzy set Techniques. Imperial College Press (2007).
- Malczewski J., Propagation of errors in multicriteria location analysis: A case study. In: G. Fandel and T. Gal (eds.) Multiple Criteria Decision Making. Springer, Berlin Heidelberg New York, (1997) 154-155.
- Malczewski J., GIS and Multicriteria Decision Analysis. USA and Canada, John Wiley & Sons (1999).
- Malczewski J, Multi-objective Decision Support Including Sensitivity Analysis. Available on: http://www.iiasa.ac.at/~marek/ ftppub/MM/eolss_mcma.pdf (2001).
- Mamdani EH and Gaines BR 1981. Fuzzy Reasoning and its Applications. London: Academic Press.
- Marks LA Dunn EG Keller JM and Godsey LD., Multiple Criteria Decision Making (MCDM) using fuzzy logic: An innovative approach to sustainable agriculture. IEEE Proceedings of ISUMA-NAFIPS ’95, Missouri-Columbia, USA (1995).
- Mesdaghi M., Management of Iran’s Rangelands. Mashhad: Imam Reza University (1995).
- Miller DJ, Rangeland management in the Hindu Kush-Himalayas. International Centre for Integrated Mountain Development (ICIMOD). Available on: http://www.icimod.org/focus/rangelands/range3.htm (2005).
- Mitchell JE, Joyce LA and Bryant LD., Applicability of Montreal process criteria and indicators to rangelands. VIth International Rangeland Congress Proceedings (1999) 1: 183-184.
- Petrovic-Lazarevic S and Abraham A., Hybrid fuzzy-linear programming approach for multi criteria decision making problems. International Journal of Neural, Parallel & Scientific Computations (2003) 11: 53-68.
- Pitz GF and McKillip J., Decision Analysis for Program Evaluators. Beverly Hills, CA: Sage (1984).
- Pohekar SD and Ramachandran M., Application of multi-criteria decision making tosustainable energy planning-A review. Renewable and Sustainable Energy Reviews (2004) 8: 365-381.
- Redfearn DD and Bidwell TG., Stocking rate: the key to successful livestock production. Available on: http://www.osuextra.com (2004).
- Roe EM, Viewpoint: on rangeland carrying capacity. Journal of Range Management (1997) 50: 467-472.
- Sands DM., Farming systems research: clarification of terms and concepts. Expl Agric (1986) 22: 87-104.
- Srebotnjak T., The role of environmental statisticians in environmental policy: the case of performance measurement. Environmental Science and Policy (2007) 10: 405-418.
- Shaner WW, Philip PF and Schmehl WR., Farming Systems Research and Development: Guidelines for Developing Countries. Westview Press (1982).
- Silvert W, Ecological impact classification with fuzzy sets. Ecological Modelling (1997) 96: 1-10.
- Silvert W, Fuzzy indices of environmental conditions. Ecological Modelling (2000) 130: 111-119.
- Starr MK and Zeleny M., Multiple Criteria Decision Making. Amsterdam: North Holland Publishing Company (1977).
- Stuth JW and Lyons BG., Decision Support Systems for the Management of Grazing Lands: Emerging Issues. Cornforth: The Parthenon Publishing Group Inc (1993).
- Tagaki T and Sugeno M., Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man and Cybernetics (1985) 15: 116-132.
- The Concise Encyclopedia of Economics., Biography of Vilfredo Pareto (1848-1923) Available on: http://www.econlib.org/library/ Enc/bios/Pareto.html (2007).
- Umrani AP., Sustainable approaches for rangeland management and livestock production in Pakistan. PhD Thesis, Agriculture Department, Aberdeen University UK (1998).
- van den Berg J., Fuzzy methodologies for evaluating sustainable development. ICMCS Conference, Nigeria: Lagos (2004).
- Wainwright J and Mulligan M., Environmental Modelling: Finding Simplicity in Complexity. New York: John Wiley & Sons (2004).
- Walker JW., Viewpoint: grazing management and research now and in the next millennium. Journal of Range Management (1995) 48: 350-357.
- Walker JW and Hodgkinson KC., Grazing management: New technologies for old problems. Available on: http://sanangelo.tamu.edu/walker/incpaper.htm (2000).
- Wang H Johnson TR and Zhang J., UEcho: A model of Uncertainty Management in Human Abductive Reasoning. Proceedings of Twentieth Annual Meeting of the Cognitive Science Society. Hillsdale, NJ Lawrence Erlbaum (1998).
- Zadeh LA., Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transactions on Systems, Man, and Cybernetics (1973) 1: 28-44.
- Zimmermann HJ., Fuzzy Set Theory and its Applications (Third Edition). Boston: Kluwer Academic Publishers (1996).






