Predictive Modeling of Extreme Weather Forecasting Events: an LSTM Approach.
1
Department of Electronics,
Yashavantarao Chavan College of Science,
Karad,
Maharashtra
India
2
Department of Electronics,
Shivaji University,
Kolhapur,
Maharashtra
India
Corresponding author Email: sas_eln@unishivaji.ac.in
DOI: http://dx.doi.org/10.12944/CWE.19.1.17
Copy the following to cite this article:
Sarwade M. P, Shinde S. A, Patil V. S. Predictive Modeling of Extreme Weather Forecasting Events: an LSTM Approach. Curr World Environ 2024;19(1). DOI:http://dx.doi.org/10.12944/CWE.19.1.17
Copy the following to cite this URL:
Sarwade M. P, Shinde S. A, Patil V. S. Predictive Modeling of Extreme Weather Forecasting Events: an LSTM Approach. Curr World Environ 2024;19(1).
Download article (pdf)
Citation Manager
Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 2023-09-18 |
|---|---|
| Accepted: | 2024-04-25 |
| Reviewed by: | 
 Amanuel Kumsa
Amanuel Kumsa
|
| Second Review by: |

 Javad Esfanjani
Javad Esfanjani
|
| Final Approval by: | Dr. R K Aggarwal |
Introduction
Accurate rainfall prediction is of critical importance in various fields due to its substantial impact on agriculture, water resource management, environmental planning, and disaster alertness. While classic statistical algorithms like regression modeling are commonly employed in regions with consistent climatic conditions, they often struggle to effectively capture non-linear and complex rainfall patterns. Recurrent Neural Networks of the Long Short-Term Memory have shown to be a particularly promising tool for rainfall prediction. LSTM networks address challenges like the vanishing gradient problem, thereby enabling the modeling of long-term dependencies in sequential data. This study contributes to the ongoing advancements in rainfall prediction methodologies by focusing on LSTM networks, meeting the growing demand for precision and reliability in weather forecasting applications. Research has demonstrated that traditional statistical models like regression, multiple regression, ARIMA, and linear regression can in fact be effective in predicting rainfall patterns, especially in regions with consistent climatic conditions. While traditional statistical algorithms and ML techniques have been extensively studied in the literature for rainfall prediction 1,2. Classic statistical algorithms face limitations when dealing with non-linear and complex rainfall patterns. This is where methods for ML are useful. In non-linear and complex systems, ML methods such as ANNs, SVMs, and decision trees have proven to be more effective in forecasting rainfall patterns3,4. Among the machine learning algorithms, RNNs and their variants, such as LSTM networks, have gained significant attention in rainfall prediction due to their ability to handle temporal dependencies and non-linearity5,6. Prediction relies heavily on back-propagation as it allows neurons to make predictions by storing the weights that are appropriate for a certain input range. Such a scenario is used to estimate monthly rainfall for Indonesia's Kalimantan area using a Back-propagating Neural Network (BPNN) with the lowest possible error7. Local predictions depend on historical data, present weather conditions, and mathematical models, whereas global predictions rely on satellite data, ground-based observations, and climate models. The most effective method varies based on the application and available data. Although machine learning and artificial intelligence techniques have the potential to improve prediction accuracy, they require large amounts of training data and can be challenging to interpret. Advances in technology and data collection will continue to drive progress in this field8. These studies provide a diverse range of approaches for predicting rainfall using machine learning techniques.
Researcher Mishra et al.9 focus on the creation and evaluation of ANN models for time-series data-based rainfall prediction, which is a commonly used approach for analyzing rainfall patterns. Miao et al. 10apply LSTM for predicting short-term fog based on weather conditions, construction and study of ANN models for forecasting rainfall based on time-series data, which can be useful in mitigating the risks associated with reduced visibility during foggy weather conditions. Finally, Endalie et al. 11 propose a method for heavy rainfall prediction using the Gini index in decision trees, which provides a simple and effective approach for predicting heavy rainfall events. Overall, these studies highlight the potential of machine learning techniques for improving rainfall prediction accuracy; It has a number of uses, including managing water resources, managing floods, and farming.
The LSTM architecture, which was pioneered by Hochreiter et al.12, is widely utilized due to it's able to arbitrarily retain or forget data, but it has weaknesses such as vanishing gradient problems as well as elevated computational costs.
In summary, while classic statistical algorithms are suitable for predicting rainfall patterns in regions with consistent climates, machine learning algorithms, particularly LSTM networks, offer a promising avenue for improving accuracy in non-linear and complex systems. The ongoing efforts to enhance the performance of RNNs underscore the importance of LSTM and attention mechanisms in the field of machine learning, showcasing their potential across a wide range of tasks.
Methodology
Understanding Recurrent Neural Networks (RNN):
RNNs are dynamic systems featuring a recurrent hidden unit designed to preserve information about past elements in a sequence13. At each time step t, the hidden state ht is determined using the current input xt and the preceding hidden state ht-1. The transformation from input sequences to output sequences involves the utilization of non-linear activation functions and adjustable parameters. Despite their effectiveness, RNNs encounter challenges with the vanishing/exploding gradient problem during the training process 14-16.
Long Short-Term Memory Architecture
The LSTM aims to overcome the vanishing gradient issue by introducing a specialized memory cell. This cell functions as a gated leaky neuron, featuring a self-connection regulated by another unit responsible for determining when to clear the memory. As shown in figure 1 within the LSTM unit, various gates are incorporated, including the forget gate, tanh layer, input gate, and output gate utilized for computing candidate values.
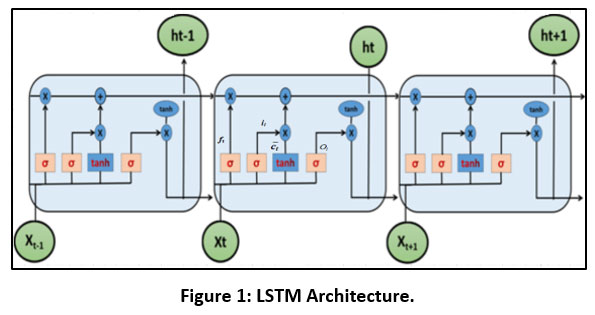 | Figure 1: LSTM Architecture.
|
The candidate vector ??, the cell state ??, the output gate ??, the forget gate f?, and the input gate i , are all involved. The forget, input, and output gates are represented by the letters f?, i?, and ??, respectively, in the preceding picture. The gates are based on a straightforward instinct:
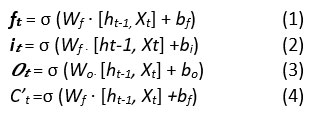
Next, the internal state of the cell is calculated as:
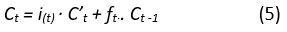
The internal cell state is then filtered out of the cell's final output, or ht.

The forget gate determines which information from the cell state should be discarded, based on the input and previous hidden state.
The forget and input gates are then used to update the cell state, and the output gate determines which data is sent to the new hidden state.
The forget and input gates are then used to update the cell state, and the output gate determines which data is sent to the new hidden state17-20.
Training and Parameterization
LSTM units are trained using backpropagation through time (BPTT) with gradient descent optimization.
Parameters such as weights (W), biases (b), and gate activation functions are optimized during training to minimize prediction errors.
Hyperparameters, such as the quantity of LSTM layers, hidden elements, and learning rates, are adjusted by the application of methods like as grid search and random search.
By following this methodology, LSTM networks enable accurate and reliable rainfall predictions, which have various applications in agriculture, water resource management, and disaster preparedness.
Location of Study
The Kolhapur district has been selected as the focal point for data collection and analysis. The data were sourced from the Zonal Agricultural Research Station (ZARS), located in Shenda Park, Kolhapur 21,22. The geographical coordinates for this location are 16.673 latitude and 74.237 longitudes as shown in figure 2. Rainfall, temperature, and humidity data are used for prediction, with preprocessing techniques like cleaning and normalization applied. Rainfall, relative humidity I and II, minimum and maximum temperatures (tmax and tmin) are examples of parameters.
 | Figure 2: Rainfall data from the Zonal Agriculture Research Station, Shenda Park, Kolhapur21.
|
Data Pre-Processing
Data preprocessing for meteorological data involves several steps, including data cleaning, which entails identifying and rectifying data errors and missing values. This step is crucial for transforming and normalizing the data, facilitating easier analysis and enhancing result accuracy. The dataset used in this study spans from January 2015 to December 2021.
Initially, the data is plotted to detect any empty or abnormal data points. For instance, Figure 3.A illustrates the maximum temperature (Tmax) from January 2015 to December 2021, revealing anomalies on March 2 and 10, 2017, with recorded temperatures of 353.3°C and 335.2°C, respectively. These outliers are corrected using the moving average method. Similarly, Figure 3.B depicts the minimum temperature (Tmin) data, highlighting an unrealistic reading of 50.4°C on July 24, 2016, which is also rectified using the moving average method. Additionally, Figure 4 displays Tmax and Tmin plotted together, uncovering unusual temperature fluctuations on December 17, 2018, which are adjusted accordingly. Figures 3.C and 3.D present relative humidity datasets, which do not require cleaning and proceed to the subsequent stage of data preprocessing.
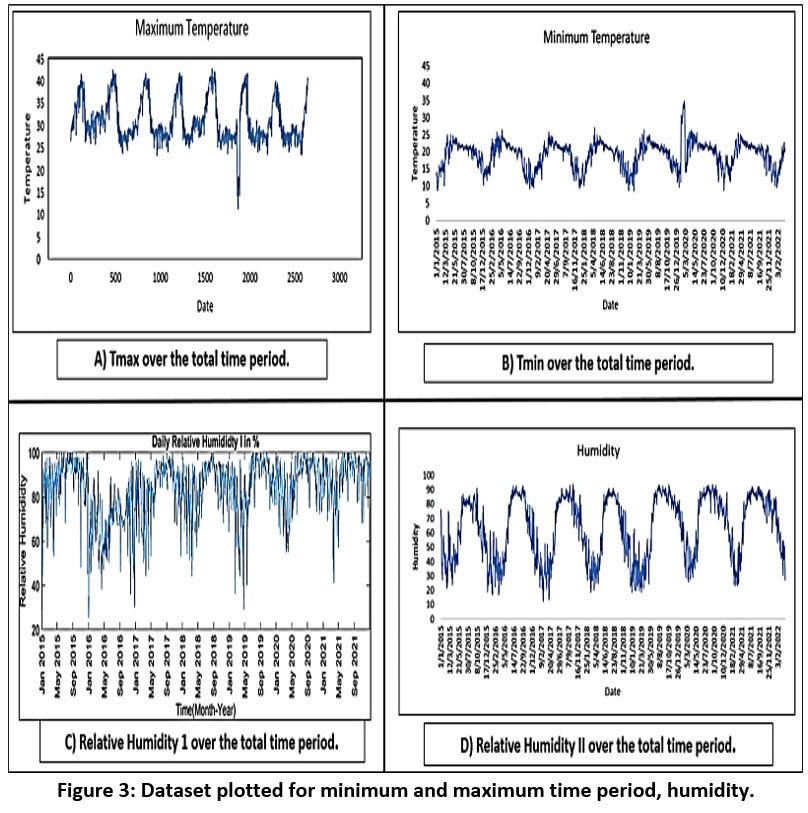 | Figure 3: Dataset plotted for minimum and maximum time period, humidity.
|
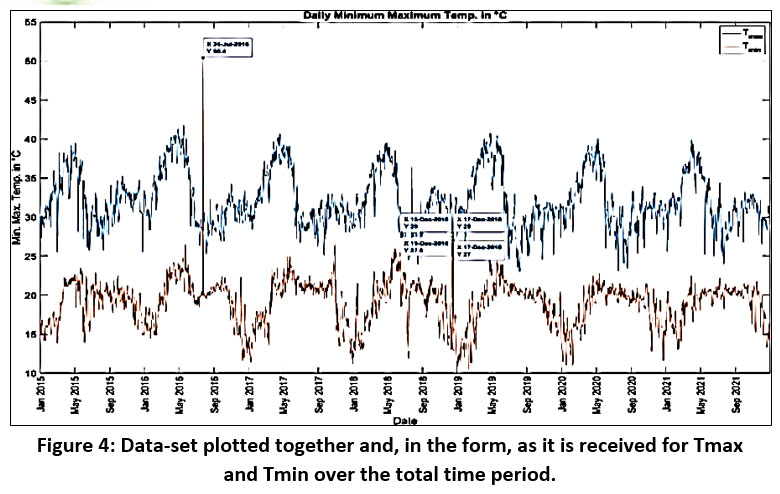 | Figure 4: Data-set plotted together and, in the form, as it is received for Tmax and Tmin over the total time period.
|
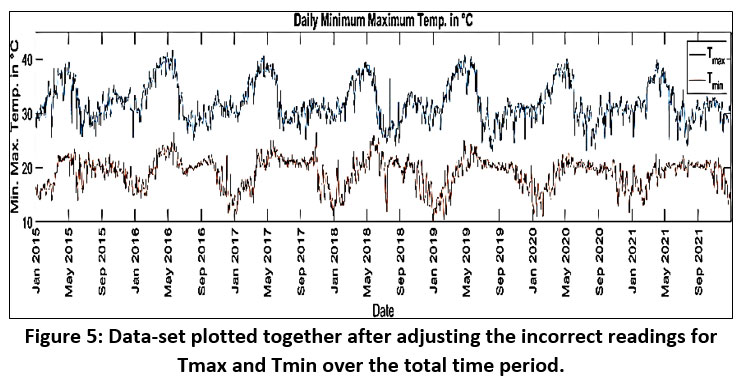 | Figure 5: Data-set plotted together after adjusting the incorrect readings for Tmax and Tmin over the total time period.
|
Feature Scaling
Feature scaling is a critical preprocessing step in deep learning, aiming to normalize the range of features. The two primary techniques are Min-Max scaling (Normalization) and Standardization. While Standardization is more robust to outliers, Min-Max scaling preserves the original data distribution. For long-range weather data spanning years, normalization is preferred to maintain the distribution form 23-26. The graphs illustrating the dataset before and after normalization are presented in Figure 6 (a, b).
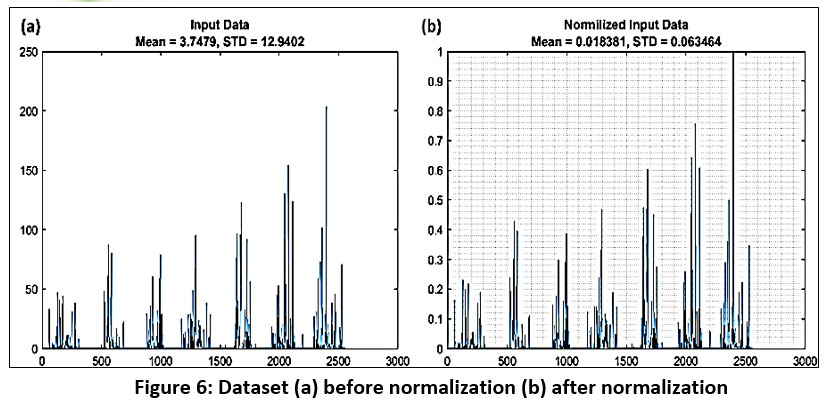 | Figure 6: Dataset (a) before normalization (b) after normalization.
|
LSTM Training and Analysis Methodology
This section outlines the workflow of LSTM module structures for rainfall prediction, detailing both implementation and validation approaches. Figure 7 illustrates the strategy employed to implement LSTM for rainfall prediction and the processing flow involved. Before LSTM implementation, data preprocessing is conducted, which includes data correction using moving averages and feature scaling using normalization methods 27. After preprocessing the data, the following strategy is implemented to develop the LSTM module for rainfall prediction.
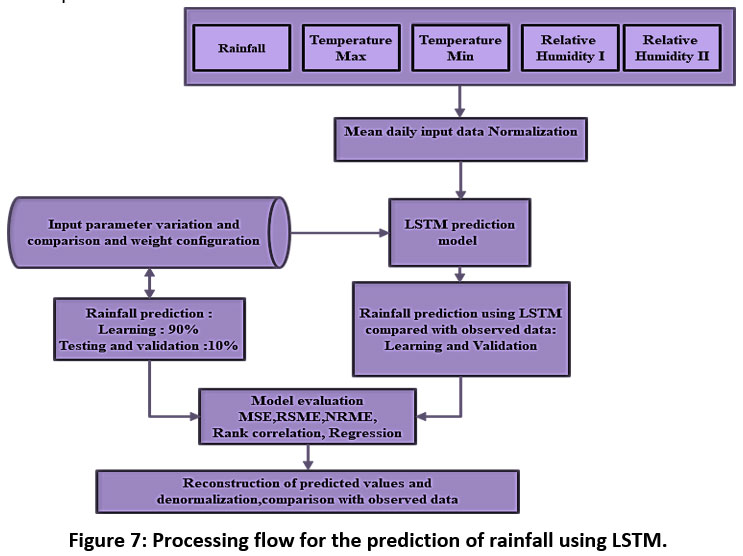 | Figure 7: Processing flow for the prediction of rainfall using LSTM.
|
LSTM: Training and Evaluation
The LSTM module is constructed with 400 hidden layers and trained over 200 epochs, resulting in a total of 6200 iterations with 31 iterations per epoch. Rainfall predictions are generated using five meteorological datasets following the training process. For training, 90% of the dataset is utilized, while three distinct testing scenarios are employed: self-testing (90%), separate testing (10%), and full dataset testing (100%). These testing scenarios allow for a thorough assessment of the LSTM model's efficiency and provide insights into how well it predicts rainfall under various settings 28-30.
Result and Discussion
The study assesses the LSTM model's performance in rainfall prediction. Figure 8(a) illustrates rank correlation computation for each dataset segment, reflecting the model's predictive capability. The graphs present target and output values for training, self-testing, separate testing, and the entire datasets. LSTM achieves a rank correlation of 0.6284 using 90% of the training data, indicating acceptable performance. Further analyses validate LSTM's commendable prediction accuracy. Figure 8(b) showcases rank correlation for test data, providing additional support for LSTM's effectiveness. Extending the analysis to all available data, Figure 8(c) demonstrates LSTM's overall superiority in rainfall prediction, with potential for further enhancement through larger meteorological datasets.
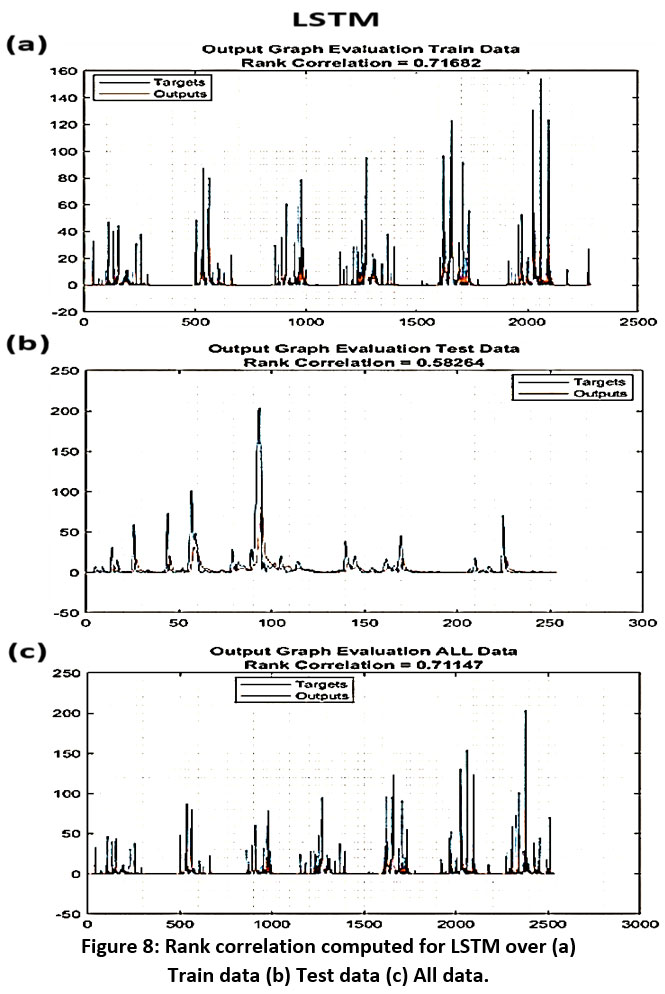 | Figure 8: Rank correlation computed for LSTM over (a) Train data (b) Test data (c) All data.
|
Evaluation Matrices
For LSTM, to evaluate prediction ability of the modules, for evaluation matrices is computed. Table I shows the values computed for RMS, NRMSE and MSE for all the portions of datasets for LSTM module.
Table 1: Performance Matrices computed using LSTM module over different portions of data-set.
ANN | Data set portion | Predicted Rainfall (mm) | |||
MSE | RMSE | NRMSE | R2 | ||
LSTM | 90% training data | 92.1839 | 9.6012 | 2.8115 | 0.24496 |
10% testing data | 374.246 | 19.3454 | 2.7499 | 0.17093 | |
All dataset | 120.423 | 10.9738 | 2.9051 | 0.23517 | |
Analysis of Evaluation Matrices
In this work, the assessment metrics of the LSTM module were examined in detail. For the training, testing, and total datasets, MSE, RMSE, and NRMSE were calculated. The results indicated that the LSTM module yielded an MSE of 92.183 and 120.423 for the 90% training dataset and the entire dataset, respectively. However, for the testing dataset, the MSE increased significantly to 374.246 due to the presence of outlier values. Similarly, the RMSE values exhibited a corresponding increase in error for the testing dataset. It's important to acknowledge that outlier values within the dataset can greatly influence and amplify the error values.
Regression model-based Analysis
The regression analysis of the LSTM module demonstrates an acceptable R-squared value of approximately 0.23517 for both the training and entire datasets (Fig. 9a, c). However, a decrease in the R-squared value is noticeable for the testing dataset (Fig. 9b), suggesting poor performance primarily due to outlier points. While the model exhibits strong performance on the training and entire datasets, there is room for improvement specifically on the testing dataset. Furthermore, it is imperative to consider the complexity of the model to prevent overfitting and ensure better performance on testing data.
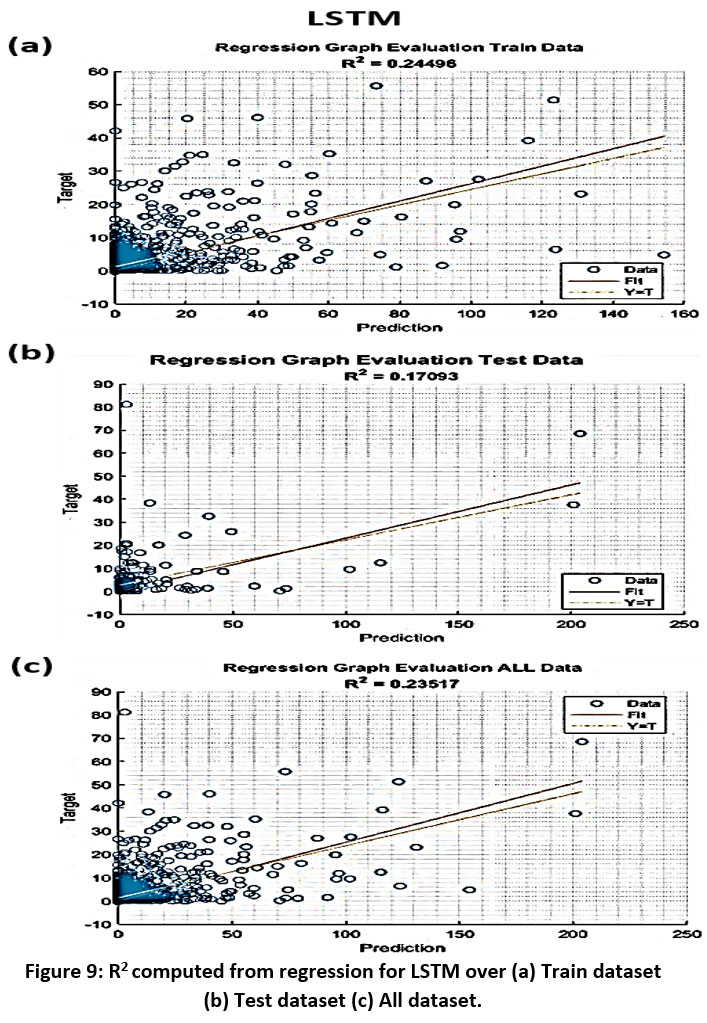 | Figure 9: R2 computed from regression for LSTM over (a) Train dataset (b) Test dataset (c) All dataset.
|
Conclusion
This study advances rainfall prediction methodologies using the LSTM method. The models, which incorporate rainfall, temperature, and humidity, demonstrate robust performance in predicting rainfall probabilities. Simulated results indicate a high probability of accurate predictions, particularly in nonlinear and complex scenarios. The validity of these results was established through rigorous testing, revealing a strong rank correlation of 0.58264 for test data and 0.71147 for all data, showcasing the effectiveness of the LSTM-based approach in handling temporal and nonlinear data.
Furthermore, the simulated outcomes show encouraging results, with an MSE of 92.1839 and an R2 value of 0.24496 throughout the whole dataset. Despite the presence of outlier points in the dataset, our model exhibits a prediction accuracy of 71.147%, as evidenced by a rank correlation of 0.71147 for all data.
Acknowledgements
The authors express gratitude to Shivaji University for granting permission to conduct the Ph.D. research work. Additionally, they extend their appreciation to the Zonal Agricultural Research Station (ZARS), Shenda Park, Kolhapur, situated at 16.673 latitude and 74.237 longitude, for generously providing the rainfall data essential for this study.
Funding Sources
This research work received no financial support.
Conflict of Interest
The authors declare that there is no conflict of interest.
Authors’ Contribution:
Author contributions for the mentioned individuals could be summarized as follows:
Meena P Sarwade: Conceptualization, Methodology, Resource allocation, Software development.
Santhosh A Shinde: Validation, Formal analysis, Investigation, Supervision during the project.
Vaishali S Patil: Original drafting of the manuscript, Data curation, Visualization of results, Project administration.
Ethics Approval Statement
No ethics approval was required for this study as it did not involve human or animal participants .
Data Availability Statement
The dataset used for the modeling includes rainfall data collected from the Zonal Agricultural Research Station (ZARS), Shenda Park, Kolhapur, available with nominal charges.
References
- Chen S., Jiang Y., Li J. Rainfall prediction using improved least squares support vector machines. J Appl Math. 2015; 2015:1-7.
- Miao C., Sun Q., Zhang A., Yang T. An effective algorithm for rainfall prediction using a hybrid model. J Hydrology. 2017; 548:704-713.
- Nagesh K. D., Srinivas V.V., Sreekanth J. Comparison of artificial neural network and regression models for prediction of rainfall in a humid tropical river basin. Hydrological Processes. 2004;18(4):801-813.
- Chandrasekar A., Giridharan R., Dhivya R. A comparative study of machine learning techniques for rainfall prediction. J Ambient Intell Humaniz Comput. 19;10(7):2465-2476.
- Zhang Y., Zhang S., Qiao F., Huang Y. An improved long short-term memory (LSTM) network for precipitation prediction. J Hydrology. 2021; 593:125844.
- Zhang Y., Zhu Y., Cheng J., Guo J. Precipitation prediction using long short-term memory neural network. J Hydrology. 2017; 548:499-507.
- Poornima, S., & Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere, 2019; 10(11), 668.
CrossRef - Parashar N., Johri P. Short-Term Temperature and Rainfall Prediction at Local and Global Spatial Scale: A Review. In: 2021 ICACITE. March 2021:742-746. IEEE.
CrossRef - Mishra N., Soni H. K., Sharma S., Upadhyay A. K. Development and analysis of artificial neural network models for rainfall prediction by using time-series data. Int J Intell Syst Appl. 2018;12(1):16.
CrossRef - Miao K. C., Han T. T., Yao Y. Q., Lu H., Chen P., Wang B., Zhang J. Application of LSTM for short term fog forecasting based on meteorological elements. Neurocomputing. 2020; 408:285-291.
CrossRef - Endalie D., Haile G., Taye W. Deep learning model for daily rainfall prediction: case study of Jimma, Ethiopia. Water Supply. 2022;22(3):3448-3461.
CrossRef - Hochreiter S., Schmidhuber J. Long short-term memory. Neural computation. 1997; 9(8):1735-1780.
CrossRef - Goodfellow I., Bengio Y., Courville A. Deep learning. MIT Press; 2016; 419-438.
- Graves A. Generating sequences with recurrent neural networks. arXiv preprint arXiv: 2013; 1308.0850.
- Chung J., Gulcehre C., Cho K., Bengio Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:2014; 1412.3555; 2014.
- Lipton ZC, Berkowitz J, Elkan C. A critical review of recurrent neural networks for sequence learning. arXiv preprint arXiv:2015; 1506.00019.
- Gers F.A., Schmidhuber J., Cummins F. Learning to forget: Continual prediction with LSTM. Neural computation. 1999;12(10):2451-2471.
CrossRef - Gharavian D., Saberi M., Khaki S. A. Forecasting daily rainfall using LSTM neural networks. Theor and App Climatology. 2020;139(3-4):1753-1763. doi:10.1007/s00704-019-03091-w
- Ioffe S., Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: ICML-15. 2015:448-456.
- Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Machine Learning Res. 2014;15(1):1929-1958.
- Google Maps. "Rainfall data is collected from the Zonal Agricultural”
- Research Station, Shenda Park, Kolhapur located at 16.67314658446148, 74.23746962134479 latitude and longitude." Link to Google Maps. Accessed (Jan. 2024).
- Steichen T. J., Cox N. J. A note on the concordance correlation coefficient. The Stata Jour. 2002;2(2):183-189.
CrossRef - Géron A. Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems. O'Reilly Media, Inc. 2019.
- Bengio, Y., Goodfellow, I. J., & Courville, A. Deep learning. MIT Press. 2016.
- Chollet F. Deep learning with Python. Manning Publications. 2018.
- Pedregosa F., Varoquaux G., Gramfort A., Michel, V., Thirion, B., Grisel, O., ... & Duchesnay, É. Scikit-learn: Machine learning in Python. J Machine Learning Res. 2011; 12:2825-2830.
- Wei W., Liu L., Wang H., Lu X. A novel long short-term memory neural network for remaining useful life estimation. Sensors. 2018;18(7):2214.
- Patil V. S., Shinde S. A., Dhawale N. M. Smart Phone Camera based Weighing Scale for Kitchens in Household Applications. In Jour of Phy: Conference Series 2021. IOP Publishing. Vol. 1921, No. 1, p. 012025
CrossRef - Patil V. S., Shinde S. A., Dhawale N. M. A review on determination of soil organic matter and soil moisture content using conventional methods and image processing techniques. In 2021 IEEE PuneCon. 2021; 01-06.
CrossRef






